Tags
- 완전검색
- drf
- distinct
- outer join
- Article & User
- SQL
- 통계학
- 백트래킹
- Tree
- 큐
- DB
- Django
- Queue
- count
- create
- migrations
- regexp
- 트리
- N:1
- 스택
- Vue
- M:N
- delete
- update
- 쟝고
- 이진트리
- stack
- 뷰
- ORM
- 그리디
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
Gaussian Elimination (가우스 소거법) 본문
가우스 소거법(Gaussian Elimination)은 연립 선형 방정식을 푸는 체계적이고 일반적인 방법입니다.
핵심 아이디어는 행(row) 단위의 연산을 통해 계수 행렬을 계단 형태(row echelon form)로 바꾸고, 거기서부터 역방향 대입(back-substitution)을 통해 해를 구하는 것입니다.
예시
다음과 같은 연립방정식을 생각해 보겠습니다:

이를 행렬로 표현하면:

이제 이 augmented matrix(확장 행렬)에 대해 행 연산(row operations)을 적용합니다.
사용 가능한 행 연산 3가지
- 어떤 두 행을 서로 바꿀 수 있습니다.
- 한 행에 상수를 곱할 수 있습니다 (단, 0은 제외).
- 한 행에 다른 행의 배수를 더하거나 뺄 수 있습니다.
이 세 가지 연산은 방정식의 해를 바꾸지 않고 행렬을 단순화할 수 있게 도와줍니다.
목표: Row Echelon Form (계단 형태)
가우스 소거법의 첫 번째 단계는 계단 형태로 바꾸는 것입니다.
예:
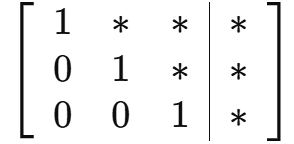
이런 식으로 아래로 내려갈수록 0이 늘어나도록 만듭니다. 그 후에는 역방향 대입(back-substitution)을 사용하여 해를 역순으로 구합니다.
'데이터 사이언스 > 선형대수학' 카테고리의 다른 글
| Equations and 3 Unknowns (3개의 방정식과 3개의 미지수) (0) | 2025.05.04 |
|---|---|
| Equations and 2 Unknowns (2개의 방정식과 2개의 미지수) (0) | 2025.05.03 |
| Lines and Planes (직선과 평면) (0) | 2025.05.02 |




